さあ,ボウリング講座の理論編です.ここでは,わたしがボウリング理論の最も基礎であると考えている「スパットボウリング」について説明します.
スパット理論とは
スパット理論は,「狙ったところにボールを投げる」ための理論です. 特に,2投目にスペアと取るときには,この理論を知っているかどうかで,大きな差が出ます. ぜひ,スパット理論によるボールコースの計算方法を覚えてください.
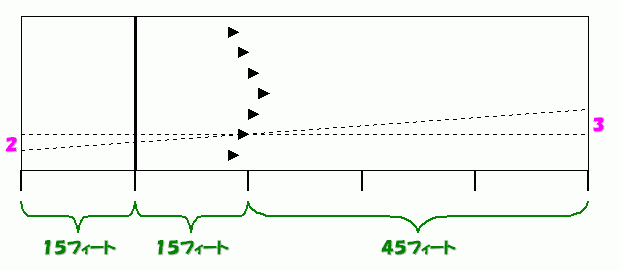
下に,レーンの概形を書き直して再掲しておきます. スパットボウリングとは,図のように2:3の相似三角形から導かれるボウリング理論です.
基本
上の図のように,レーンはスパットを中心にして2:3 に分かれています. その比によりスパットを中心に三角形を書くと,2つの相似三角形を書くことができます. その相似三角形の辺の長さの比は,もちろん2:3であるので,アプローチで2だけ右方向へきっちりとずらして立ち,きっちりと同じ歩き方をし,きっちりと同じスパットの上にボールを投げると,ピンに当たる時に3だけ左方向へずれます. 本当にきっちりとするというのは難しいですけど,練習してコントロールがよくなると,かなりこの理論は役立ちます.
ボールコースの計算方法
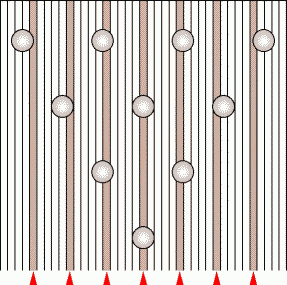
スパットは上図のように5枚ごとにマークされていて,ピンは5.5枚の間隔で置かれています. そのため,ポケットコースにボールがいくときに通るスパットと,アプローチでの立つ位置が決まっていれば,その同じスパットにボールを通す場合,この2:3の比率を考えることで,様々なピンに当てる位置を調整することができます.
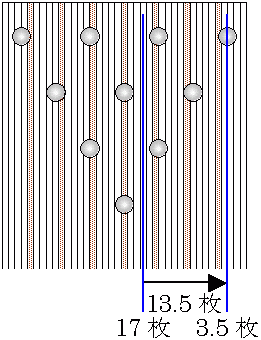
例えば,10枚目(右から2つ目)のスパットを使ってポケット(ここでは17枚目とします)にボールが必ずいくように投げられるものと. この場合に,10番ピンをどのように取るか,上図を使って考えます.
まず,10番ピンがどこにあるかを計算します. 1番ピンは真ん中の20枚目にあり,ピンとピンの横間隔は5.5枚であるので,
20 - 5.5 × 3 = 3.5
となり,3.5枚目に10番ピンがあることがわかります. そこで,ポケット(17枚目)と10番ピンとの間隔は,
17 - 3.5 = 13.5
なり,13.5枚の間隔があることがわかります.
このことから,ポケットコースから10番ピンに右へ13.5枚ボールのコースをずらすためには,相似三角形の辺の比が2:3であることから,
13.5 × 2 ÷ 3 = 9枚
となり,アプローチ上で9枚だけ左にずれて立てば,10ピンを取ることができる,ということになります.
また,立ち位置を固定して,スパットだけを移動すると,今度は 2:5 の相似三角形ができあがります. そのため,スパットを一つ移動すると,12.5枚ずれてピンにあたります.
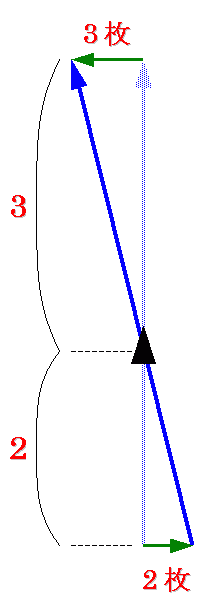
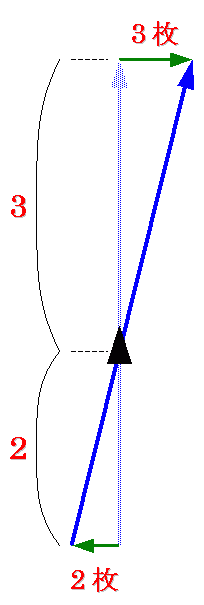
もっと簡単に説明します. 下の図1のようなコースをいつも投げている場合を考えます.
図2のように右に板目2枚ずれた位置から投げると,ボールはピンに当たるところで左に3枚ずれます.
図3のように左に板目2枚ずれた位置から投げると,ボールはピンに当たるところで右に3枚ずれます.
これがスパット理論の計算方法の一番簡単で基本的なものです.

このように簡単に書いてしまいましたが,すべてはこのような計算により成り立ちます. あとは,この応用によって,すべてのピン(スプリットを除く)を取ることが可能となります.
これが,スパットボウリングの理論です.
補足:立ち位置
スパット理論では,アプローチに立つ位置をしっかりと決めなければなりません. 立ち位置の決め方は,2種類あります.

右端を板目に合わせる
左端を板目に合わせる
どちらがいいかは一概には言えないですが,わたしは右投げなので右側に合わせています. 各個人の好みに合わせてください.
ボウリングでは,このスパット理論があるために,「スパットにボールを通す」ということにもっとも集中力を使います.
初心者は,まずは10枚目(右から2つ目)のスパットを通すということを心がけるようにして下さい. 毎回同じように投げることができるようになれば,必ず上記の理論の通りにボールが行くはずです.
ある程度安定して投げられるようになったら,微調整を行います. 10枚目のスパットを通ってボールが狙う位置よりも左方向へずれたなら,立つ位置を左へずらします. 逆に,ボールが右方向へずれたなら,立つ位置を右へずらします.
そして,たくさん投げ込むうちに,自分に最適な立ち位置と投げる目標となるスパットが見つかると思います. 自分に最適な立ち位置が見つかったら,目標のスパットへ確実にボールを通せるようにさらに練習しましょう.
立つ位置を計算しよう
1投目でポケットコースを投げるときに狙うスパットか,狙う板目のどちらを選択します. そして,2投目で狙うピンを選択したら「計算」ボタンを押してください. 狙う板目を固定した場合に立ち位置をどれだけ移動するか,あるいは立ち位置を固定した場合に狙う板目をどれだけ変更するか,計算します.
















































